Main > Efficiently handling endian differences using negative memory addressing
A common issue in emulation and virtualization is endian difference between the host and guest architectures. Common cases of that are N64, Wii, GC, PS3, and XBOX360 that are big endian emulated on x86/x64 (PC) that is little endian.
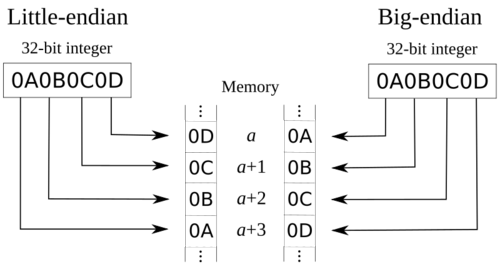
What is endian order?
Endian order is the order in which bytes are stored in memory. For small numbers all is good and great as they fit in a single byte, but when we have to split number into multiple bytes there are many options on how to arrange the information. Of course, the industry has managed to settle into two different, standards, as byte ordering is such an important issue. Bah.
First, there is the little endian order, which the only option in x86, and supported by most other architectures. In little endian order the “least” important bytes come first. So when you have to rite “1024” in 4 bytes you write 1024 = 2 * 256 + 0 -> 0, 2, 0, 0 (= 0 1 + 2 * 256 + 0 *256 * 256 + 0256256256). While many architectures are “bi-endian”, little is generally preferred because development is done generally in PCs and it is generally easier to work with the same endian order on development and target platforms.
Then, there is the big endian order. PowerPC and motorolla (and Apple) have traditionally used this format, and it used to be more popular in older hardware. I suspect it is for that reason that it is also called the “network byte order”, and it is used in many protocols (incl. various parts of tcp/ip headers). This order is more natural to how we write numbers on paper and the most important digits come first. So, “1024” is stored as 1024 = 2 * 256 + 0 = 0, 0, 2, 0 (= 0 256256256 + 0256256 + 2256 + 0*1). IBM goes even further as the bit numbering is reversed in powerpc cpu manuals, with bit 0 being the MSB and bit 31 the LSB, in a 4 byte word.
Of course, endianess is one of those irritating issues an emulator has to address. The reason it is so irritating is the silliness of it, how often you need to convert data, and that sometimes conversion is a slow operation with unreliable performance across cpu families. Converting from one endian to the other is just a matter of swapping the bytes: [a, b, c, d] -> [d, c, b, a].
A neat solution - “The XOR trick”
A typical niceish way to handle the endian issue is to have the memory “pre swapped”. This means that you pick the most common access size (usually 32 or 64 bits) and the bytes in memory are arranged such that operations using that access size don’t need any conversion.
To illustrate this
Assuming we have bytes #0 to #11, corresponding to the first 12 bytes of XBOX 360’s memory, and that we want to store these for fast access on our amazing xbox 360 emulator. Of course, we soon find out that swapping on access is ugly and slow, let’s prematurely over-think the issue for the shake of illustration. Also please note that in array access I use byte offset, not index number (so mem_16[8] means two bytes starting from byte number 8).
Xbox 360 memory layout
[ #0, #1, #2, #3, #4, #5, #6, #7, #8, #9, #10, #11, #12, ... ]
Awesome xbox 360 emulator memory layout with “32 bit pre-swapping”
[ #3, #2, #1, #0, #7, #6, #5, #4, #11, #10, #9, #8, ... ]
As you might have noticed, bytes are swapped every 32 bits (4 bytes). This makes memory access on 32 bit units very fast, as
mem[0]= [#3, #2, #1, #0]
mem[4]= [#7, #6, #5, #4]
// no need to swap bytes for endian, it is already done!
Now smaller accesses sizes becomes an issue though. For 16 bit accesses
mem_16[0] = [#3, #2]
mem_16[2] = [#1, #0]
This is obviously wrong, as the [0] should have been [2], and [2] should have been [0]. Moving to byte accesses makes this even worse as
mem_8[0] = #3
mem_8[1] = #2
mem_8[2] = #1
mem_8[3] = #0
At last, 64 bit accesses still require us partially swapping things around
mem_64[0] = [#3, #2, #1, #0, #7, #6, #5, #4]
//Damn, So close. Correct order is [#7, #6, #5, #4, #3, #2, #1, #0]
As you can see this quickly becomes a headache. To solve the smaller access issues we can use “the xor trick” to swap the order of the entries, and xor is cheapish.
mem_u8[address ^ 3] -> [0] maps to [3] returing #0 as expected
mem_u16[address ^ 2] -> [0] maps to [2] returning [#1, #0] as expected
But on modern cpus bswap is as almost fast as xor. And we still have to swap anything more than 32 bits.
There’s also the complication that you can’t just blindly read data from the filesystem as you have to swap anything that goes to memory, and you can’t write data without de-pre-swapping (it’s the same operation as pre-swapping), unaligned access, and other subtle issues. So quite clearly, not an ideal situation…
A neater solution - “Negative memory addressing”
A long while ago I was pondering about getting nullDCe to run on the wii. I ended up using 32-bit pre-swapping (there’s actually a video of it running on youtube). During that period I had an idea that would solve the endian issue more elegantly, but I didn’t end up using it because SH4 worked nicely enough with the XOR trick. (I also got bored after a while.)
Memory addressing usually starts from the beginning of memory, so [0] is the first byte, [1] is the second byte, [2] is the 3rd byte, and so on. While doing weird math on addresses to optimize my memory dispatch code, I realized that if you access the data in the “other way around” it you have a mirrored, swapped view of it. And by “the other way around” I mean pointing to the end of the memory, and [-1] being the last byte, [-2] the 2nd from the end, [-3] the third from the end, and so forth.
Awesome xbox 360 emulator memory layout with “Negative Addressing”
[ #11, #10, #9, #8, #7, #6, #5, #4, #3, #2, #1, #0 ]
Also the memory access has to be modified to mem_8[ length - 1 - addr ]. we can just add length-1 (constant) to mem_8 (also constant) and name the result mem_8e. Then we can simplify the expression to mem_8e[-addr].
Let’s try with 8 bit access first
mem_8e[-0] = mem_8[12-1-0] = mem_8[11] = #0 //Yay!
mem_8e[-1] = mem_8[12-1-1] = mem_8[10] = #1 //Yay!
mem_8e[-2] = mem_8[12-1-2] = mem_8[9] = #2 //Yay!
mem_8e[-3] = mem_8[12-1-3] = mem_8[8] = #3 //Yay!
mem_8e[-11] = mem_8[12-1-11] = mem_8[0] = #11 //Yay!
Looks to be working alright!
Doing the same for 16 bit access, mem_16e[-a] -> mem_16[len-1-a] results in
mem_16e[-0] = mem_16[11] = [#0, ?]
//Woops! Wrong! Off by one error :'(
But, if we modify the equation to mem_16e[-a] -> mem_16[len-2-a]
mem_16e[-0] = mem_16[10] = [#1, #0]
mem_16e[-2] = mem_16[8] = [#3, #2]
//Now all is good!
And then for 32 bits, mem_32e[-a] -> mem_32[len-4-a]
mem_32e[-0] = mem_32[8] = [#3, #2, #1, #0]
mem_32e[-4] = mem_32[4] = [#7, #6, #5, #4]
//Yup, still works
And even for 64 bits, with mem_64e[-a] = mem_64[len-8-a]
mem_64e[-0] = mem_64[4] = [#7, #6, #5, #4, #3, #2, #1, #0]
//Amazing, right?
It also happens to work for misaligned access
mem_64e[-1] = mem64[3] = [#8, #7, #6, #5, #4, #3, #2, #1]
The generic formula is mem[length - access_size_in_bytes - address] and works for arbitrary long accesses, including vectors and everything. While some the issues of having a “not linear” memory view persist - like special handling for reading/writing to filesystem/textures, imo this is much more elegant than the XOR trick. Also in many cpus you can fold some of the work on address generation, reducing the cost. Since the operations are linear, you can also keep side-counting pointers or even negate the value of registers that are used as pointers inside a basic block. This can be really beneficial when you have many memory accesses on the same block.
As a sidenote, this might be also useful for implementing endian handling in FIFOs such as the Dolphin GPU FIFO. I should try that at some point…
Lots of thanks on benvanik for starting the xenia project, that’s how all of this resurfaced from some dusty corner of my mind.
So, that’s it for today. Do leave comments! I’d love to know of other clever ways to solve this!
(I know, very long article. Will write a short one next time. About unicorns and rainbows. It’s gonna be short and elegant like glimpsing into the heavens. Or maybe not. I still love unicorns though.)